Estimated time: 20 minutes plus review questions
Take-home points: Understanding key properties and dynamics of sound waves is essential for optimal use of clinical echocardiography.
-
- A sound wave consists of regions of rarefaction and compression of the medium through which it travels.
- The wave speed v, frequency f, and wavelength λ of a wave are related according to v =fλ.
- The resolution of an ultrasound image is roughly the wavelength of the sound waves used to produce it.
- Wave speed depends on the medium in which the wave travels (air, water, tissue), so resolution depends on the frequency chosen and the medium.
How sound waves are generated by a transducer (or anything else….)
-
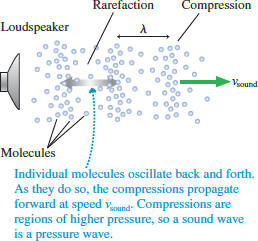
- A sound wave is generated by a vibrating object, such as the piezoelectric crystal of an ultrasound transducer.
- As the crystal oscillates, it compresses the air or material ahead of it as it moves forward. That compressed air/material continues to move forward due to its inertia.
- The crystal then reverses direction and moves back, leaving a rarefied (less dense) region following behind the compressed region.
- The result is a traveling series of compressed and rarefied regions as shown in Figure 1, which we call a wave.
- If the original vibrations are sinusoidal, the density along the direction of travel follows a sinusoidal pattern, as shown in Figure 2; this pattern moves at a steady speed.
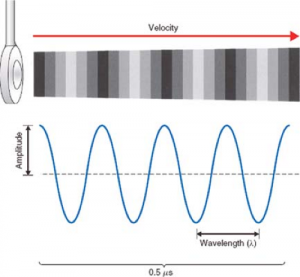
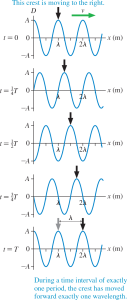
Figure 2: Sinusoidal pressure wave shown both by color scale and by a graph of pressure vs time. Fig.. 26-1 from Echocardiography, by Perrino,Popescu, and Skubas. - Figure 3 shows a series of snapshots of such a wave as it travels, as graphs of the wave pressure vs position. Pressure is measured relative to ambient pressure. A wave “crest” is at the location of maximum compression of the wave.
This simulation (requires Java) demonstrates this process.
Amplitude, frequency, wavelength, and resolution
-
- The more compression and rarefaction compared to the baseline density, the greater the amplitude of the wave (the height of the peak of the curve, labeled A in Figure 2). The amount of energy contained in the wave increases as the wave’s amplitude increases.
- The frequency, f, is the inverse of the time period of the oscillation T, which is the length of time that passes between the start of each oscillation: f = 1/T. The base unit of frequency is cycles per second, sometimes called Hertz. 1 Hz = 1 cycle/s.
-
- We perceive the frequency of an audible sound wave as its musical pitch.
- Humans can hear sound waves with frequencies ranging from 20 Hz to 20 kHz (kilohertz or 103Hz).
- Clinical ultrasound frequencies, which are typically a few MHz (megahertz, meaning 1 million Hz = 106 Hz), cannot be heard by humans.
- The period T is different from the return time t we introduced in Lesson 1; T is a property of the sound wave itself. It is controlled by the transducer: T is the time required for the oscillator that produces the sound wave to undergo a single vibration, which dictates the length of time of all the resulting oscillations of the air or medium.
-
- The wavelength λ (“lambda” — the Greek form of the letter l) of a sinusoidal wave is the distance between neighboring peaks, labeled in the bottom panels of Figures 2 and 3.
- The wavelength is the limiting factor for the resolution of an ultrasound image; with optimal transducer design, the smallest structures that can be distinguished in the image are at least roughly λ in size, often 1.5λ or 2λ.
Speed of sound waves in various substances (“media”)
-
- Sound waves can travel through any substance (such as air, water, or tissue), often called the “medium” of the wave. (Sound waves cannot travel in a vacuum, such as exists in outer space, because there is no matter to undergo compression and rarefaction.)
- The wave speed v, frequency f, and wavelength λ of a wave are related according to
v =fλ.
The units of this equation work out: speed has units of distance/time, frequency has units of 1/time, and wavelength has units of distance. - During one wave period T, a sound wave moves forward by exactly one wavelength, as seen by comparing the top and bottom panels of Figure 2.

Table 1. Speed of sound in various media. - The speed of sound in a medium depends on how it responds to compression. Roughly speaking, the stiffer the medium, the faster sound travels. Table 1 gives values.
- The resolution of an ultrasound image is determined by the wavelength in the tissue being imaged, not in air.
-
- Notice that the speed in tissue is roughly four times that in air. Consequently, although a 1 MHz ultrasound wave has a wavelength in air of
its wavelength in soft tissue is roughly four times greater, because increasing v by some factor will also increase the wavelength by the same factor. The result is λin tissue= 1.54 mm. - The clinical ultrasound frequency range (typically 1-10 MHz) corresponds to wavelengths in tissue ranging from roughly 0.2 to 2 mm.
- Notice that the speed in tissue is roughly four times that in air. Consequently, although a 1 MHz ultrasound wave has a wavelength in air of
Measures of energy in ultrasound waves: power and intensity
-
- A useful concept is the rate of energy delivery by the wave per unit time, or the power delivered by the wave. Typical units for power are Watts (W).
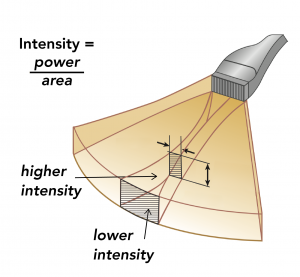
- The intensity of a wave is its power divided by the area over which it spreads (Figure 4). For audible sound, intensity corresponds to its loudness.
- An ultrasound beam typically spreads out as it travels, so its intensity decreases with distance of travel even without absorption.
- In clinical ultrasound, intensity is commonly measured in W/cm2, but because the clinical range of power (P) and intensity (I) is so large, they are also commonly expressed on a logarithmic scale relative to a standard value (P0 or I0), using decibels.
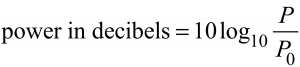
- Ultrasound power and intensity are clinically relevant for two reasons:
-
- Excessive power transmitted to tissue may result in heating and damage. This is most relevant for transesophageal echocardiograms.
- Power affects how far the sound wave penetrates, as discussed in the next lesson.
-
Review questions:
- What is the frequency of the ultrasound wave represented in Figure 2 above? (Answer)
- When an ultrasound pulse enters the body of a patient, does the wavelength in the patient’s tissues increase, decrease, or remain the same (compared to the wavelength in air outside the patient)? (Answer)
- If the frequency being used for an echo study is doubled from 1 MHz to 2 MHz, how does the wavelength of the sound waves in the patient change? (Answer)
- Suppose the first ultrasound image acquired of a particular structure doesn’t provide enough detail to see the structure clearly. To achieve higher resolution, if attenuation was not an issue, would you increase or decrease the ultrasound frequency with which you are imaging? (Answer)
- Explain the two causes of attenuation (reduction of intensity) of an ultrasound wave as it travels, and why only one of these causes a reduction of power. (Answer)